ଧ୍ରୁବୀକରଣ ହେଉଛି ଆଣ୍ଟେନାର ମୌଳିକ ବୈଶିଷ୍ଟ୍ୟ ମଧ୍ୟରୁ ଗୋଟିଏ। ଆମକୁ ପ୍ରଥମେ ସମତଳ ତରଙ୍ଗର ଧ୍ରୁବୀକରଣ ବୁଝିବାକୁ ପଡିବ। ତା'ପରେ ଆମେ ମୁଖ୍ୟ ପ୍ରକାରର ଆଣ୍ଟେନା ଧ୍ରୁବୀକରଣ ବିଷୟରେ ଆଲୋଚନା କରିପାରିବା।
ରେଖୀୟ ଧ୍ରୁବୀକରଣ
ଆମେ ଏକ ସମତଳ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗର ଧ୍ରୁବୀକରଣକୁ ବୁଝିବା ଆରମ୍ଭ କରିବା।
ଏକ ପ୍ଲାନାର ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ (EM) ତରଙ୍ଗର ଅନେକ ଗୁଣ ଅଛି। ପ୍ରଥମଟି ହେଉଛି ଶକ୍ତି ଗୋଟିଏ ଦିଗରେ ଯାତ୍ରା କରେ (ଦୁଇଟି ଅର୍ଥୋଗୋନାଲ ଦିଗରେ କୌଣସି କ୍ଷେତ୍ର ପରିବର୍ତ୍ତନ ହୁଏ ନାହିଁ)। ଦ୍ୱିତୀୟଟି ହେଉଛି, ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଏବଂ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ଏବଂ ଅର୍ଥୋଗୋନାଲ। ବୈଦ୍ୟୁତିକ ଏବଂ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସମତଳ ତରଙ୍ଗ ପ୍ରସାରଣ ଦିଗ ପ୍ରତି ଲମ୍ବ। ଉଦାହରଣ ସ୍ୱରୂପ, ସମୀକରଣ (1) ଦ୍ୱାରା ପ୍ରଦତ୍ତ ଏକକ-ଆବୃତ୍ତି ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର (E କ୍ଷେତ୍ର) ବିଚାର କରନ୍ତୁ। ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର +z ଦିଗରେ ଯାତ୍ରା କରୁଛି। ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର +x ଦିଗରେ ନିର୍ଦ୍ଦେଶିତ। ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର +y ଦିଗରେ।
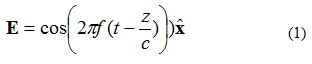
ସମୀକରଣ (1) ରେ, ଏହି ନୋଟେସନ୍ କୁ ପଡ଼ାନ୍ତୁ: । ଏହା ଏକ ୟୁନିଟ୍ ଭେକ୍ଟର (ଲମ୍ବ ଏକ ଭେକ୍ଟର), ଯାହା କୁହେ ଯେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ବିନ୍ଦୁ x ଦିଗରେ ଅଛି। ଚିତ୍ର 1 ରେ ସମତଳ ତରଙ୍ଗ ଦର୍ଶାଯାଇଛି।
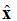
ଚିତ୍ର ୧. +z ଦିଗରେ ଗତି କରୁଥିବା ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରର ଗ୍ରାଫିକାଲ୍ ଉପସ୍ଥାପନା।
ଧ୍ରୁବୀକରଣ ହେଉଛି ଏକ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରର ଟ୍ରେସ୍ ଏବଂ ପ୍ରସାରଣ ଆକୃତି (ଆକୃତି)। ଉଦାହରଣ ସ୍ୱରୂପ, ସମତଳ ତରଙ୍ଗ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ସମୀକରଣ (1) ବିଚାର କରନ୍ତୁ। ଆମେ ସମୟର ଏକ କାର୍ଯ୍ୟ ଭାବରେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର (X,Y,Z) = (0,0,0) ଥିବା ସ୍ଥାନକୁ ପର୍ଯ୍ୟବେକ୍ଷଣ କରିବା। ଏହି କ୍ଷେତ୍ରର ଆମ୍ପ୍ଲିଚ୍ୟୁଡ୍ ସମୟର ଅନେକ ସ୍ଥାନରେ ଚିତ୍ର 2 ରେ ପ୍ଲଟ୍ କରାଯାଇଛି। କ୍ଷେତ୍ରଟି "F" ଫ୍ରିକ୍ୱେନ୍ସିରେ ଦୋଳନ କରୁଛି।
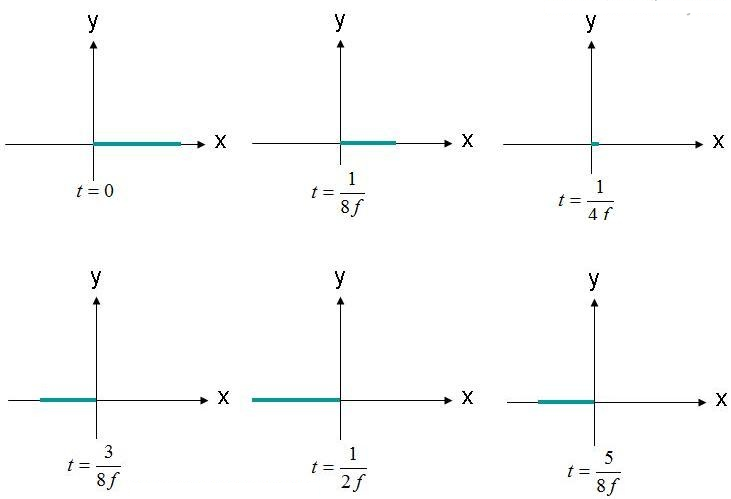
ଚିତ୍ର 2. ବିଭିନ୍ନ ସମୟରେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର (X, Y, Z) = (0,0,0) ପର୍ଯ୍ୟବେକ୍ଷଣ କରନ୍ତୁ।
ଉତ୍ପତ୍ତି ସ୍ଥାନରେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ପରିଲକ୍ଷିତ ହୁଏ, ଆମ୍ପ୍ଲିଚ୍ୟୁଡ୍ ଭାବରେ ଆଗକୁ ପଛକୁ ଦୋଳନଶୀଳ ହୁଏ। ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ସର୍ବଦା ସୂଚିତ x-ଅକ୍ଷ ସହିତ ଥାଏ। ଯେହେତୁ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଗୋଟିଏ ରେଖା ସହିତ ରଖାଯାଏ, ଏହି କ୍ଷେତ୍ରକୁ ରେଖୀୟ ଭାବରେ ଧ୍ରୁବୀୟ ବୋଲି କୁହାଯାଇପାରେ। ଏହା ସହିତ, ଯଦି X-ଅକ୍ଷ ଭୂମି ସହିତ ସମାନ୍ତରାଳ ହୋଇଥାଏ, ତେବେ ଏହି କ୍ଷେତ୍ରକୁ ଭୂସମାନ୍ତର ଧ୍ରୁବୀୟ ଭାବରେ ମଧ୍ୟ ବର୍ଣ୍ଣନା କରାଯାଏ। ଯଦି କ୍ଷେତ୍ରଟି Y-ଅକ୍ଷ ସହିତ ଦିଗନ୍ତ ହୋଇଥାଏ, ତେବେ ତରଙ୍ଗକୁ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ବୋଲି କୁହାଯାଇପାରେ।
ରେଖୀୟ ଧ୍ରୁବୀୟ ତରଙ୍ଗଗୁଡ଼ିକୁ ଏକ ଭୂସମାନ୍ତର କିମ୍ବା ଭୂଲମ୍ବ ଅକ୍ଷ ସହିତ ନିର୍ଦ୍ଦେଶିତ କରିବାର ଆବଶ୍ୟକତା ନାହିଁ। ଉଦାହରଣ ସ୍ୱରୂପ, ଚିତ୍ର 3 ରେ ଦେଖାଯାଇଥିବା ପରି ଏକ ରେଖା ସହିତ ଏକ ସୀମା ସହିତ ଏକ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ତରଙ୍ଗ ମଧ୍ୟ ରେଖୀୟ ଧ୍ରୁବୀୟ ହେବ।
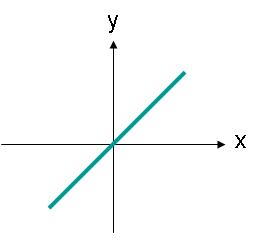
ଚିତ୍ର 3. ଏକ ରେଖୀୟ ଧ୍ରୁବୀୟ ତରଙ୍ଗର ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ବିସ୍ତାର ଯାହାର ଗତିପଥ ଏକ କୋଣ।
ଚିତ୍ର 3 ରେ ଥିବା ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରକୁ ସମୀକରଣ (2) ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯାଇପାରିବ। ବର୍ତ୍ତମାନ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରର ଏକ x ଏବଂ y ଉପାଦାନ ଅଛି। ଉଭୟ ଉପାଦାନ ଆକାରରେ ସମାନ।
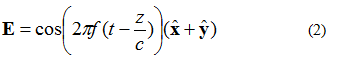
ସମୀକରଣ (2) ବିଷୟରେ ଗୋଟିଏ କଥା ମନେରଖିବା ଉଚିତ ଯେ ଦ୍ୱିତୀୟ ପର୍ଯ୍ୟାୟରେ xy-ଉପାଦାନ ଏବଂ ଇଲେକ୍ଟ୍ରୋନିକ୍ କ୍ଷେତ୍ର। ଏହାର ଅର୍ଥ ହେଉଛି ଉଭୟ ଉପାଦାନର ସବୁବେଳେ ସମାନ ଆମ୍ପ୍ଲିଚ୍ୟୁଡ୍ ଥାଏ।
ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ
ଏବେ ଧରିନିଅ ଯେ ଏକ ସମତଳ ତରଙ୍ଗର ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ସମୀକରଣ (3) ଦ୍ୱାରା ଦିଆଯାଇଛି:
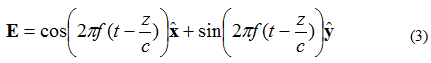
ଏହି କ୍ଷେତ୍ରରେ, X- ଏବଂ Y-ମୌଳିକଗୁଡ଼ିକ ପର୍ଯ୍ୟାୟ ବାହାରେ 90 ଡିଗ୍ରୀ ଅଛନ୍ତି। ଯଦି କ୍ଷେତ୍ରକୁ ପୂର୍ବ ପରି (X, Y, Z) = (0,0,0) ଭାବରେ ପର୍ଯ୍ୟବେକ୍ଷଣ କରାଯାଏ, ତେବେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ବନାମ ସମୟ ବକ୍ର ଚିତ୍ର 4 ରେ ନିମ୍ନରେ ଦେଖାଯାଇଥିବା ପରି ଦେଖାଯିବ।
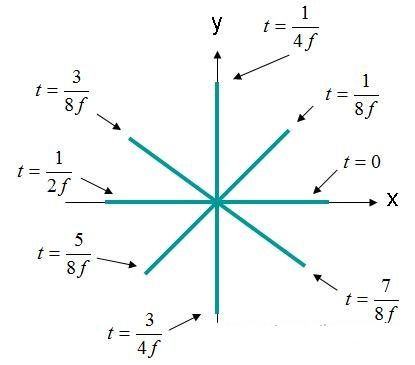
ଚିତ୍ର 4. ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଶକ୍ତି (X, Y, Z) = (0,0,0) EQ ଡୋମେନ୍। (3)।
ଚିତ୍ର ୪ ରେ ଥିବା ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଏକ ବୃତ୍ତରେ ଘୂରୁଛି। ଏହି ପ୍ରକାରର କ୍ଷେତ୍ରକୁ ଏକ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ତରଙ୍ଗ ଭାବରେ ବର୍ଣ୍ଣନା କରାଯାଇଛି। ବୃତ୍ତାକାର ଧ୍ରୁବୀୟକରଣ ପାଇଁ, ନିମ୍ନଲିଖିତ ମାନଦଣ୍ଡ ପୂରଣ କରିବାକୁ ପଡିବ:
- ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ ପାଇଁ ମାନକ
- ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରରେ ଦୁଇଟି ଅର୍ଥୋଗୋନାଲ (ଲମ୍ବ) ଉପାଦାନ ରହିବା ଆବଶ୍ୟକ।
- ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରର ଅର୍ଥୋଗୋନାଲ ଉପାଦାନଗୁଡ଼ିକର ସମାନ ଆମ୍ପ୍ଲିଚ୍ୟୁଡ୍ ରହିବା ଆବଶ୍ୟକ।
- ଚତୁର୍ଭୁଜ ଉପାଦାନଗୁଡ଼ିକ ପର୍ଯ୍ୟାୟ ବାହାରେ 90 ଡିଗ୍ରୀ ହେବା ଆବଶ୍ୟକ।
ଯଦି ତରଙ୍ଗ ଚିତ୍ର 4 ସ୍କ୍ରିନରେ ଯାତ୍ରା କରାଯାଏ, ତେବେ କ୍ଷେତ୍ର ଘୂର୍ଣ୍ଣନକୁ ଘଣ୍ଟାକଣ୍ଟାର ବିପରୀତ ଦିଗରେ ଏବଂ ଡାହାଣ ହାତରେ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ (RHCP) କୁହାଯାଏ। ଯଦି କ୍ଷେତ୍ରକୁ ଘଣ୍ଟାକଣ୍ଟାର ଦିଗରେ ଘୂରାଯାଏ, ତେବେ କ୍ଷେତ୍ରଟି ବାମ ହାତରେ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ (LHCP) ହେବ।
ଅଣ୍ଡାକାର ଧ୍ରୁବୀକରଣ
ଯଦି ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରରେ ଦୁଇଟି ଲମ୍ବ ଉପାଦାନ ଥାଏ, ପର୍ଯ୍ୟାୟ ବାହାରେ 90 ଡିଗ୍ରୀ କିନ୍ତୁ ସମାନ ପରିମାଣର, ତେବେ କ୍ଷେତ୍ରଟି ଅଣ୍ଡାକାର ଭାବରେ ଧ୍ରୁବୀକରଣ ହେବ। ସମୀକରଣ (4) ଦ୍ୱାରା ବର୍ଣ୍ଣିତ +z ଦିଗରେ ଯାତ୍ରା କରୁଥିବା ଏକ ସମତଳ ତରଙ୍ଗର ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରକୁ ବିଚାର କଲେ:
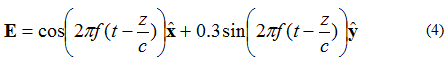
ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଭେକ୍ଟରର ଅଗ୍ରଭାଗ ଯେଉଁ ବିନ୍ଦୁରେ ଧାରଣା କରିବ ତାହାର ସ୍ଥାନ ଚିତ୍ର 5 ରେ ଦିଆଯାଇଛି।
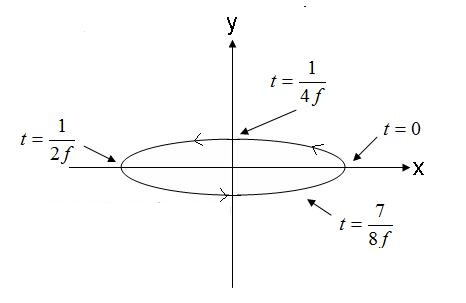
ଚିତ୍ର 5. ଅଣ୍ଡାକାର ଧ୍ରୁବୀକରଣ ତରଙ୍ଗ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରକୁ ପ୍ରେରଣା ଦିଅନ୍ତୁ। (4)।
ଚିତ୍ର 5 ରେ ଥିବା କ୍ଷେତ୍ରଟି, ଘଣ୍ଟାକଣ୍ଟାର ବିପରୀତ ଦିଗରେ ଗତି କରୁଛି, ଯଦି ଏହା ସ୍କ୍ରିନରୁ ବାହାରକୁ ଯାତ୍ରା କରୁଛି ତେବେ ଡାହାଣ ହାତିଆ ଅଣ୍ଡାକାର ହେବ। ଯଦି ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଭେକ୍ଟର ବିପରୀତ ଦିଗରେ ଘୂରେ, ତେବେ କ୍ଷେତ୍ରଟି ବାମ ହାତିଆ ଅଣ୍ଡାକାର ଧ୍ରୁବୀୟ ହେବ।
ଅଧିକନ୍ତୁ, ଅଣ୍ଡାକାର ଧ୍ରୁବୀକରଣ ଏହାର ବିଚିତ୍ରତାକୁ ବୁଝାଏ। ପ୍ରମୁଖ ଏବଂ କ୍ଷୁଦ୍ର ଅକ୍ଷର ବିକୃତି ସହିତ ବିଚିତ୍ରତାର ଅନୁପାତ। ଉଦାହରଣ ସ୍ୱରୂପ, ସମୀକରଣ (4) ରୁ ତରଙ୍ଗ ବିଚିତ୍ରତା ହେଉଛି 1/0.3= 3.33। ଅଣ୍ଡାକାର ଧ୍ରୁବୀକରଣ ତରଙ୍ଗଗୁଡ଼ିକ ପ୍ରମୁଖ ଅକ୍ଷର ଦିଗ ଦ୍ୱାରା ଆହୁରି ବର୍ଣ୍ଣନା କରାଯାଇଛି। ତରଙ୍ଗ ସମୀକରଣ (4) ର ଏକ ଅକ୍ଷ ଅଛି ଯାହା ମୁଖ୍ୟତଃ x-ଅକ୍ଷକୁ ନେଇ ଗଠିତ। ଧ୍ୟାନ ଦିଅନ୍ତୁ ଯେ ପ୍ରମୁଖ ଅକ୍ଷ ଯେକୌଣସି ସମତଳ କୋଣରେ ହୋଇପାରେ। କୋଣ X, Y କିମ୍ବା Z ଅକ୍ଷ ସହିତ ଫିଟ୍ ହେବା ଆବଶ୍ୟକ ନୁହେଁ। ଶେଷରେ, ଏହା ମନେ ରଖିବା ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ଯେ ବୃତ୍ତାକାର ଏବଂ ରେଖିକ ଧ୍ରୁବୀକରଣ ଉଭୟ ଅଣ୍ଡାକାର ଧ୍ରୁବୀକରଣର ବିଶେଷ କ୍ଷେତ୍ର। 1.0 ଅଣ୍ଡାକାର ଅଣ୍ଡାକାର ଧ୍ରୁବୀକରଣ ତରଙ୍ଗ ହେଉଛି ଏକ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ ତରଙ୍ଗ। ଅନନ୍ତ ବିଚିତ୍ରତା ସହିତ ଅଣ୍ଡାକାର ଧ୍ରୁବୀକରଣ ତରଙ୍ଗ। ରେଖିକ ଧ୍ରୁବୀକରଣ ତରଙ୍ଗ।
ଆଣ୍ଟିନା ଧ୍ରୁବୀକରଣ
ଏବେ ଆମେ ଧ୍ରୁବୀୟ ସମତଳ ତରଙ୍ଗ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ବିଷୟରେ ଅବଗତ, ଏକ ଆଣ୍ଟେନାର ଧ୍ରୁବୀୟକରଣକୁ ସରଳ ଭାବରେ ପରିଭାଷିତ କରାଯାଇଛି।
ଆଣ୍ଟେନା ଧ୍ରୁବୀକରଣ ଏକ ଆଣ୍ଟେନା ଦୂର-କ୍ଷେତ୍ର ମୂଲ୍ୟାଙ୍କନ, ଯାହା ଫଳାଫଳରେ ବିକିରଣ କ୍ଷେତ୍ରର ଧ୍ରୁବୀକରଣ। ତେଣୁ, ଆଣ୍ଟେନାଗୁଡ଼ିକୁ ପ୍ରାୟତଃ "ରେଖୀୟ ଧ୍ରୁବୀକରଣ" କିମ୍ବା "ଡାହାଣ-ହାତୀ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ ଆଣ୍ଟେନା" ଭାବରେ ତାଲିକାଭୁକ୍ତ କରାଯାଏ।
ଏହି ସରଳ ଧାରଣା ଆଣ୍ଟେନା ଯୋଗାଯୋଗ ପାଇଁ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ। ପ୍ରଥମତଃ, ଏକ ଭୂସମାନ୍ତର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଏକ ଭୂସମାନ୍ତର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ସହିତ ଯୋଗାଯୋଗ କରିବ ନାହିଁ। ପାରସ୍ପରିକ ତତ୍ତ୍ୱ ଯୋଗୁଁ, ଆଣ୍ଟେନା ଠିକ୍ ସମାନ ଭାବରେ ପ୍ରସାରିତ ଏବଂ ଗ୍ରହଣ କରେ। ତେଣୁ, ଭୂସମାନ୍ତର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନାଗୁଡ଼ିକ ଭୂସମାନ୍ତର ଧ୍ରୁବୀୟ କ୍ଷେତ୍ରଗୁଡ଼ିକୁ ପ୍ରସାରିତ ଏବଂ ଗ୍ରହଣ କରନ୍ତି। ତେଣୁ, ଯଦି ଆପଣ ଏକ ଭୂସମାନ୍ତର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନାକୁ ପହଞ୍ଚାଇବାକୁ ଚେଷ୍ଟା କରନ୍ତି, ତେବେ କୌଣସି ଗ୍ରହଣ ହେବ ନାହିଁ।
ସାଧାରଣ କ୍ଷେତ୍ରରେ, ଗୋଟିଏ କୋଣ ( ) ଦ୍ୱାରା ପରସ୍ପର ସାପେକ୍ଷରେ ଘୂର୍ଣ୍ଣିତ ଦୁଇଟି ରେଖୀୟ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ପାଇଁ, ଏହି ଧ୍ରୁବୀୟକରଣ ଅସଙ୍ଗତତା ଯୋଗୁଁ ଶକ୍ତି କ୍ଷତିକୁ ଧ୍ରୁବୀୟକରଣ କ୍ଷତି କାରକ (PLF) ଦ୍ୱାରା ବର୍ଣ୍ଣନା କରାଯିବ:
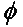
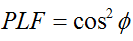
ତେଣୁ, ଯଦି ଦୁଇଟି ଆଣ୍ଟେନାର ସମାନ ଧ୍ରୁବୀକରଣ ଥାଏ, ତେବେ ସେମାନଙ୍କର ବିକିରଣକାରୀ ଇଲେକ୍ଟ୍ରନ୍ କ୍ଷେତ୍ର ମଧ୍ୟରେ କୋଣ ଶୂନ୍ୟ ହୋଇଥାଏ ଏବଂ ଧ୍ରୁବୀକରଣ ଅସଙ୍ଗତତା ଯୋଗୁଁ କୌଣସି ଶକ୍ତି କ୍ଷତି ହୁଏ ନାହିଁ। ଯଦି ଗୋଟିଏ ଆଣ୍ଟେନା ଭୂଲମ୍ବ ଧ୍ରୁବୀକରଣ ହୋଇଥାଏ ଏବଂ ଅନ୍ୟଟି ଭୂଲମ୍ବ ଧ୍ରୁବୀକରଣ ହୋଇଥାଏ, ତେବେ କୋଣ 90 ଡିଗ୍ରୀ ହୋଇଥାଏ, ଏବଂ କୌଣସି ଶକ୍ତି ସ୍ଥାନାନ୍ତରିତ ହେବ ନାହିଁ।
ଟିପ୍ପଣୀ: ଆପଣଙ୍କ ମୁଣ୍ଡ ଉପରେ ଫୋନକୁ ବିଭିନ୍ନ କୋଣକୁ ଘୁଞ୍ଚାଇବା ଦ୍ଵାରା ଏହା ବୁଝାଏ ଯେ କେତେବେଳେ ଗ୍ରହଣ ବୃଦ୍ଧି ହୋଇପାରେ। ସେଲ୍ ଫୋନ୍ ଆଣ୍ଟେନାଗୁଡ଼ିକ ସାଧାରଣତଃ ରେଖୀୟ ଭାବରେ ଧ୍ରୁବୀକରଣ ହୋଇଥାଏ, ତେଣୁ ଫୋନ୍ ଘୂରାଇବା ପ୍ରାୟତଃ ଫୋନ୍ର ଧ୍ରୁବୀକରଣ ସହିତ ମେଳ ଖାଇପାରେ, ଯାହା ଫଳରେ ଗ୍ରହଣ ଉନ୍ନତ ହୁଏ।
ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ ଅନେକ ଆଣ୍ଟେନାର ଏକ ଆଗ୍ରହ୍ୟ ବୈଶିଷ୍ଟ୍ୟ। ଉଭୟ ଆଣ୍ଟେନାର ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ ହୋଇଥାଏ ଏବଂ ଧ୍ରୁବୀକରଣ ଅସଙ୍ଗତତା ଯୋଗୁଁ ସିଗନାଲ କ୍ଷତି ହୁଏ ନାହିଁ। GPS ସିଷ୍ଟମରେ ବ୍ୟବହୃତ ଆଣ୍ଟେନାର ଡାହାଣ-ହାତ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ ହୋଇଥାଏ।
ଏବେ ଧରିନିଅନ୍ତୁ ଯେ ଏକ ରେଖୀୟ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ତରଙ୍ଗ ଗ୍ରହଣ କରେ। ସମାନ ଭାବରେ, ଧରିନିଅନ୍ତୁ ଯେ ଏକ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ରେଖୀୟ ଧ୍ରୁବୀୟ ତରଙ୍ଗ ଗ୍ରହଣ କରିବାକୁ ଚେଷ୍ଟା କରେ। ଫଳସ୍ୱରୂପ ଧ୍ରୁବୀୟ କ୍ଷତି କାରକ କ'ଣ?
ମନେରଖନ୍ତୁ ଯେ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ ପ୍ରକୃତରେ ଦୁଇଟି ଅର୍ଥୋଗୋନାଲ୍ ରେଖୀୟ ଧ୍ରୁବୀକରଣ ତରଙ୍ଗ, ପର୍ଯ୍ୟାୟ ବାହାରେ 90 ଡିଗ୍ରୀ। ତେଣୁ, ଏକ ରେଖୀୟ ଧ୍ରୁବୀକରଣ (LP) ଆଣ୍ଟେନା କେବଳ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ (CP) ତରଙ୍ଗ ପର୍ଯ୍ୟାୟ ଉପାଦାନ ଗ୍ରହଣ କରିବ। ତେଣୁ, LP ଆଣ୍ଟେନାର ଧ୍ରୁବୀକରଣ ଅସମଞ୍ଜସ୍ୟ କ୍ଷତି 0.5 (-3dB) ରହିବ। LP ଆଣ୍ଟେନାକୁ କେଉଁ କୋଣରେ ଘୂରାଯାଉ ଏହା ସତ୍ୟ। ତେଣୁ:
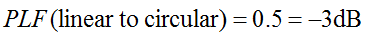
ଧ୍ରୁବୀକରଣ କ୍ଷତି କାରକକୁ କେତେକ ସମୟରେ ଧ୍ରୁବୀକରଣ ଦକ୍ଷତା, ଆଣ୍ଟେନା ମିସମେଚ କାରକ, କିମ୍ବା ଆଣ୍ଟେନା ଗ୍ରହଣ କାରକ ଭାବରେ କୁହାଯାଏ। ଏହି ସମସ୍ତ ନାମ ସମାନ ଧାରଣାକୁ ସୂଚିତ କରେ।
ପୋଷ୍ଟ ସମୟ: ଡିସେମ୍ବର-୨୨-୨୦୨୩







