ଆଣ୍ଟେନା ଦୁନିଆରେ, ଏପରି ଏକ ନିୟମ ଅଛି। ଯେତେବେଳେ ଏକ ଭୂଲମ୍ବ ଭାବରେଧ୍ରୁବୀୟ ଆଣ୍ଟେନାପ୍ରସାରଣ କରେ, ଏହା କେବଳ ଏକ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଦ୍ୱାରା ଗ୍ରହଣ କରାଯାଇପାରିବ; ଯେତେବେଳେ ଏକ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ପ୍ରସାରଣ କରେ, ଏହା କେବଳ ଏକ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଦ୍ୱାରା ଗ୍ରହଣ କରାଯାଇପାରିବ; ଯେତେବେଳେ ଏକ ଡାହାଣ-ହାତବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନାପ୍ରସାରଣ କରେ, ଏହାକୁ କେବଳ ଡାହାଣ-ହାତ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଦ୍ୱାରା ଗ୍ରହଣ କରାଯାଇପାରିବ; ଯେତେବେଳେ ଏକ ବାମ-ହାତ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ପ୍ରସାରଣ କରେ, ଏହାକୁ କେବଳ ଡାହାଣ-ହାତ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଦ୍ୱାରା ଗ୍ରହଣ କରାଯାଇପାରିବ; ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ପ୍ରସାରଣ କରେ ଏବଂ କେବଳ ବାମ-ହାତ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଦ୍ୱାରା ଗ୍ରହଣ କରାଯାଇପାରିବ।
ଆରଏଫଏମଆଇଏସଓବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ହର୍ଣ୍ଣ ଆଣ୍ଟେନା ଉତ୍ପାଦଗୁଡ଼ିକ
ତଥାକଥିତ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଆଣ୍ଟେନା ଦ୍ୱାରା ନିର୍ଗତ ତରଙ୍ଗକୁ ବୁଝାଏ, ଏବଂ ଏହାର ଧ୍ରୁବୀୟ ଦିଗ ଭୂଲମ୍ବ ଅଟେ।
ତରଙ୍ଗର ଧ୍ରୁବୀକରଣ ଦିଗ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଭେକ୍ଟରର ଦିଗକୁ ସୂଚିତ କରେ।
ତେଣୁ, ତରଙ୍ଗର ଧ୍ରୁବୀକରଣ ଦିଗ ଉଲ୍ଲମ୍ବ, ଯାହାର ଅର୍ଥ ହେଉଛି ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଭେକ୍ଟରର ଦିଗ ଉଲ୍ଲମ୍ବ।
ସେହିପରି, ଏକ ଭୂସମାନ୍ତର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ଅର୍ଥ କରେ ଯେ ତରଙ୍ଗର ଦିଗ ଅନୁଭୂମିକ, ଯାହାର ଅର୍ଥ ହେଉଛି ଏହା ନିର୍ଗତ କରୁଥିବା ତରଙ୍ଗର ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଦିଗ ପୃଥିବୀ ସହିତ ସମାନ୍ତରାଳ।
ଭୂଲମ୍ବ ଧ୍ରୁବୀକରଣ ଏବଂ ଭୂସମାନ୍ତର ଧ୍ରୁବୀକରଣ ଉଭୟ ପ୍ରକାରର ରେଖୀୟ ଧ୍ରୁବୀକରଣ।
ତଥାକଥିତ ରେଖୀୟ ଧ୍ରୁବୀକରଣ ତରଙ୍ଗର ଧ୍ରୁବୀକରଣକୁ ବୁଝାଏ, ଅର୍ଥାତ୍, ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରର ଦିଗ ଏକ ସ୍ଥିର ଦିଗରେ ସୂଚିତ କରେ। ସ୍ଥିର ଅର୍ଥ ହେଉଛି ଏହା ପରିବର୍ତ୍ତନ ହେବ ନାହିଁ।
ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ଆଣ୍ଟେନା ତରଙ୍ଗର ଧ୍ରୁବୀୟକରଣକୁ ବୁଝାଏ, ଅର୍ଥାତ୍, ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ରର ଦିଗ, ଯାହା ସମୟ ପରିବର୍ତ୍ତନ ସହିତ ଏକ ସମାନ କୋଣୀୟ ବେଗ w ରେ ଘୂରେ।
ତେବେ ବାମ-ହାତୀ ଏବଂ ଡାହାଣ-ହାତୀ ବୃତ୍ତାକାର ଧ୍ରୁବୀକରଣ କିପରି ନିର୍ଣ୍ଣୟ କରାଯାଏ?
ଉତ୍ତର ତୁମ ହାତରେ ଅଛି।
ତରଙ୍ଗ ପ୍ରସାରଣ ଦିଗରେ ବୁଢ଼ା ଆଙ୍ଗୁଠି ଦେଖାଇ ଉଭୟ ହାତକୁ ବାହାର କରନ୍ତୁ, ଏବଂ ତା’ପରେ ଦେଖନ୍ତୁ କେଉଁ ହାତର ବଙ୍କା ଆଙ୍ଗୁଠିଗୁଡ଼ିକ ଧ୍ରୁବୀକରଣ ଦିଗରେ ଘୂରୁଛି।
ଯଦି ଡାହାଣ ହାତ ସମାନ, ତେବେ ଏହା ଡାହାଣ ହାତ ଧ୍ରୁବୀକରଣ; ଯଦି ବାମ ହାତ ସମାନ, ତେବେ ଏହା ବାମ ହାତ ଧ୍ରୁବୀକରଣ।
ପରେ, ମୁଁ ତୁମକୁ ବୁଝାଇବା ପାଇଁ ସୂତ୍ର ବ୍ୟବହାର କରିବି। ଏବେ ଧର, ଦୁଇଟି ରେଖୀୟ ଧ୍ରୁବୀୟ ତରଙ୍ଗ ଅଛି।
ଗୋଟିଏ ଧ୍ରୁବୀକରଣ ଦିଗ ହେଉଛି x ଦିଗ ଏବଂ ଆମ୍ପ୍ଲିଚ୍ୟୁଡ୍ ହେଉଛି E1; ଗୋଟିଏ ଧ୍ରୁବୀକରଣ ଦିଗ ହେଉଛି y ଦିଗ ଏବଂ ଆମ୍ପ୍ଲିଚ୍ୟୁଡ୍ ହେଉଛି E2; ଉଭୟ ତରଙ୍ଗ z ଦିଗ ସହିତ ପ୍ରସାରିତ ହୁଏ।
ଦୁଇଟି ତରଙ୍ଗ ଉପରେ ରହି, ମୋଟ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ହେଉଛି:
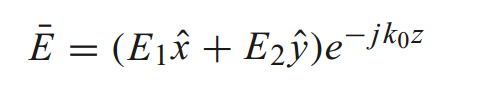
ଉପରୋକ୍ତ ସୂତ୍ରରୁ, ଅନେକ ସମ୍ଭାବନା ଅଛି:
(1) E1≠0, E2=0, ତେବେ ସମତଳ ତରଙ୍ଗର ଧ୍ରୁବୀକରଣ ଦିଗ ହେଉଛି x-ଅକ୍ଷ
(2) E1=0, E2≠0, ତେବେ ସମତଳ ତରଙ୍ଗର ଧ୍ରୁବୀକରଣ ଦିଗ ହେଉଛି y-ଅକ୍ଷ
(3) ଯଦି E1 ଏବଂ E2 ଉଭୟ ପ୍ରକୃତ ସଂଖ୍ୟା ଏବଂ 0 ନୁହେଁ, ତେବେ ସମତଳ ତରଙ୍ଗର ଧ୍ରୁବୀକରଣ ଦିଗ x-ଅକ୍ଷ ସହିତ ନିମ୍ନଲିଖିତ କୋଣ ଗଠନ କରେ:
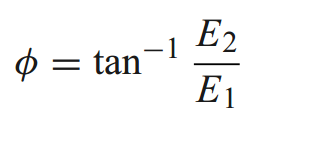
(୪) ଯଦି E1 ଏବଂ E2 ମଧ୍ୟରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପର୍ଯ୍ୟାୟ ପାର୍ଥକ୍ୟ ଥାଏ, ଯେପରି ନିମ୍ନ ଚିତ୍ରରେ ଦର୍ଶାଯାଇଛି, ତେବେ ସମତଳ ତରଙ୍ଗ ଏକ ଡାହାଣ-ହାତ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ତରଙ୍ଗ କିମ୍ବା ଏକ ବାମ-ହାତ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ତରଙ୍ଗରେ ପରିଣତ ହୋଇପାରେ।
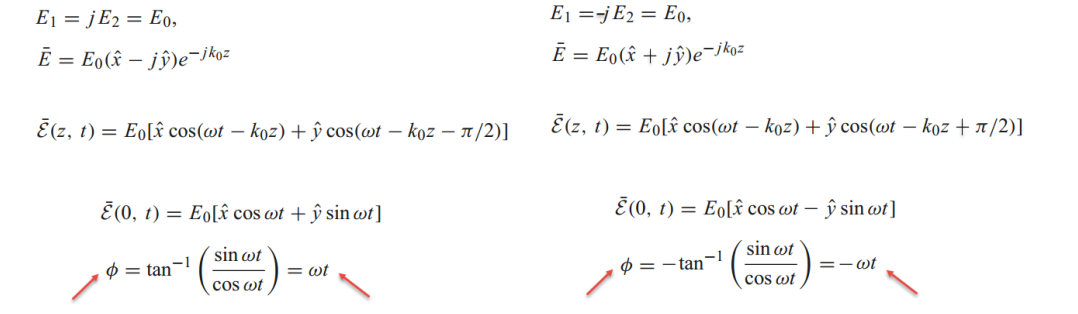
ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନାଗୁଡ଼ିକ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ତରଙ୍ଗ ଗ୍ରହଣ କରିବା ପାଇଁ ଏବଂ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ଆଣ୍ଟେନାଗୁଡ଼ିକ ଭୂଲମ୍ବ ଧ୍ରୁବୀୟ ତରଙ୍ଗ ଗ୍ରହଣ କରିବା ପାଇଁ, ଆପଣ ନିମ୍ନର ଚିତ୍ରଟି ଦେଖି ଏହାକୁ ବୁଝିପାରିବେ।
କିନ୍ତୁ ବୃତ୍ତାକାର ଧ୍ରୁବୀୟ ତରଙ୍ଗ ବିଷୟରେ କ'ଣ? ବୃତ୍ତାକାର ଧ୍ରୁବୀୟକରଣ ହାସଲ କରିବା ପ୍ରକ୍ରିୟାରେ, ପର୍ଯ୍ୟାୟ ପାର୍ଥକ୍ୟ ସହିତ ଦୁଇଟି ରେଖୀୟ ଧ୍ରୁବୀୟକରଣକୁ ସୁପରପୋଜିସନ୍ କରି ଏହା ପ୍ରାପ୍ତ ହୁଏ।
ଆଣ୍ଟେନା ବିଷୟରେ ଅଧିକ ଜାଣିବା ପାଇଁ, ଦୟାକରି ପରିଦର୍ଶନ କରନ୍ତୁ:
ପୋଷ୍ଟ ସମୟ: ମଇ-୨୧-୨୦୨୪











