ଯେତେବେଳେ କଥା ଆସେଆଣ୍ଟିନା, ଲୋକମାନେ ଯେଉଁ ପ୍ରଶ୍ନ ବିଷୟରେ ସବୁଠାରୁ ଅଧିକ ଚିନ୍ତିତ ତାହା ହେଉଛି "ପ୍ରକୃତରେ ବିକିରଣ କିପରି ହାସଲ ହୁଏ?" ସିଗନାଲ ଉତ୍ସ ଦ୍ୱାରା ସୃଷ୍ଟି ହୋଇଥିବା ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର କିପରି ଟ୍ରାନ୍ସମିସନ୍ ଲାଇନ ମାଧ୍ୟମରେ ଏବଂ ଆଣ୍ଟେନା ଭିତରେ ପ୍ରସାରିତ ହୁଏ ଏବଂ ଶେଷରେ ଆଣ୍ଟେନାରୁ "ପୃଥକ" ହୋଇ ଏକ ମୁକ୍ତ ସ୍ଥାନ ତରଙ୍ଗ ସୃଷ୍ଟି କରେ।
୧. ଏକକ ତାର ବିକିରଣ
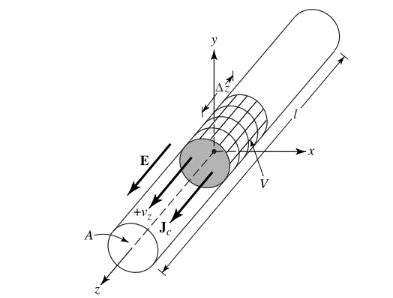
ଆସନ୍ତୁ ଧରିନେବା ଯେ ଚାର୍ଜ ଘନତ୍ୱ, qv (Coulomb/m3) ଭାବରେ ପ୍ରକାଶିତ, ଚିତ୍ର 1 ରେ ଦେଖାଯାଇଥିବା ପରି, a ର କ୍ରସ-ସେକ୍ସନାଲ୍ କ୍ଷେତ୍ରଫଳ ଏବଂ V ର ଆୟତନ ସହିତ ଏକ ବୃତ୍ତାକାର ତାରରେ ସମାନ ଭାବରେ ବଣ୍ଟନ କରାଯାଇଛି।
ଚିତ୍ର 1
V ଆୟତନରେ ମୋଟ ଚାର୍ଜ Q ଏକ ସମାନ ବେଗ Vz (m/s) ରେ z ଦିଗରେ ଗତି କରେ। ଏହା ପ୍ରମାଣିତ ହୋଇପାରେ ଯେ ତାରର କ୍ରସ ସେକ୍ସନରେ Jz ବିଦ୍ୟୁତ୍ ଘନତ୍ୱ ହେଉଛି:
Jz = qv vz (1)
ଯଦି ତାରଟି ଏକ ଆଦର୍ଶ ପରିବାହୀରେ ତିଆରି ହୋଇଥାଏ, ତେବେ ତାର ପୃଷ୍ଠରେ ବିଦ୍ୟୁତ୍ ଘନତ୍ୱ Js ହେବ:
Js = qs vz (2)
ଯେଉଁଠାରେ qs ହେଉଛି ପୃଷ୍ଠ ଚାର୍ଜ ଘନତ୍ୱ। ଯଦି ତାରଟି ବହୁତ ପତଳା ହୋଇଥାଏ (ଆଦର୍ଶ ଭାବରେ, ବ୍ୟାସାର୍ଦ୍ଧ 0), ତେବେ ତାରରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତକୁ ଏହିପରି ପ୍ରକାଶ କରାଯାଇପାରିବ:
Iz = ql vz (3)
ଯେଉଁଠାରେ ql (କୁଲମ୍ବ/ମିଟର) ହେଉଛି ପ୍ରତି ୟୁନିଟ୍ ଲମ୍ବ ପାଇଁ ଚାର୍ଜ।
ଆମେ ମୁଖ୍ୟତଃ ପତଳା ତାର ସହିତ ଜଡିତ, ଏବଂ ଉପରୋକ୍ତ ତିନୋଟି କ୍ଷେତ୍ରରେ ନିଷ୍କର୍ଷ ପ୍ରଯୁଜ୍ୟ। ଯଦି ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସମୟ-ପରିବର୍ତ୍ତନଶୀଳ ହୁଏ, ତେବେ ସମୟ ସମ୍ୱନ୍ଧରେ ସୂତ୍ର (3) ର ଡେରିଭେଟିଭ୍ ନିମ୍ନଲିଖିତ ଅଟେ:
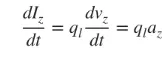
(୪)
az ହେଉଛି ଚାର୍ଜ ତ୍ୱରଣ। ଯଦି ତାରର ଲମ୍ବ l ହୁଏ, (4) କୁ ନିମ୍ନଲିଖିତ ଭାବରେ ଲେଖାଯାଇପାରିବ:
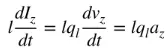
(5)
ସମୀକରଣ (5) ହେଉଛି ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଏବଂ ଚାର୍ଜ ମଧ୍ୟରେ ମୌଳିକ ସମ୍ପର୍କ, ଏବଂ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ବିକିରଣର ମୌଳିକ ସମ୍ପର୍କ। ସରଳ ଭାବରେ କହିବାକୁ ଗଲେ, ବିକିରଣ ଉତ୍ପାଦନ କରିବା ପାଇଁ, ସମୟ-ପରିବର୍ତ୍ତନଶୀଳ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ କିମ୍ବା ତ୍ୱରଣ (କିମ୍ବା ହ୍ରାସ) ରହିବା ଆବଶ୍ୟକ। ଆମେ ସାଧାରଣତଃ ସମୟ-ସହଜୋଗ ପ୍ରୟୋଗରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଉଲ୍ଲେଖ କରୁ, ଏବଂ ଚାର୍ଜକୁ ପ୍ରାୟତଃ କ୍ଷଣସ୍ଥାୟୀ ପ୍ରୟୋଗରେ ଉଲ୍ଲେଖ କରାଯାଏ। ଚାର୍ଜ ତ୍ୱରଣ (କିମ୍ବା ହ୍ରାସ) ଉତ୍ପାଦନ କରିବା ପାଇଁ, ତାରକୁ ବଙ୍କା, ଫୋଲ୍ଡ ଏବଂ ବିଚ୍ଛିନ୍ନ ହେବା ଆବଶ୍ୟକ। ଯେତେବେଳେ ଚାର୍ଜ ସମୟ-ସହଜୋଗ ଗତିରେ ଦୋଳନ କରେ, ଏହା ମଧ୍ୟ ସାମୟିକ ଚାର୍ଜ ତ୍ୱରଣ (କିମ୍ବା ହ୍ରାସ) କିମ୍ବା ସମୟ-ପରିବର୍ତ୍ତନଶୀଳ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଉତ୍ପାଦନ କରିବ। ତେଣୁ:
୧) ଯଦି ଚାର୍ଜ ଗତି ନ କରେ, ତେବେ କୌଣସି କରେଣ୍ଟ ଏବଂ ବିକିରଣ ହେବ ନାହିଁ।
୨) ଯଦି ଚାର୍ଜ ସ୍ଥିର ଗତିରେ ଗତି କରେ:
କ. ଯଦି ତାରଟି ସିଧା ଏବଂ ଅସୀମ ଲମ୍ବ ହୋଇଥାଏ, ତେବେ କୌଣସି ବିକିରଣ ହୁଏ ନାହିଁ।
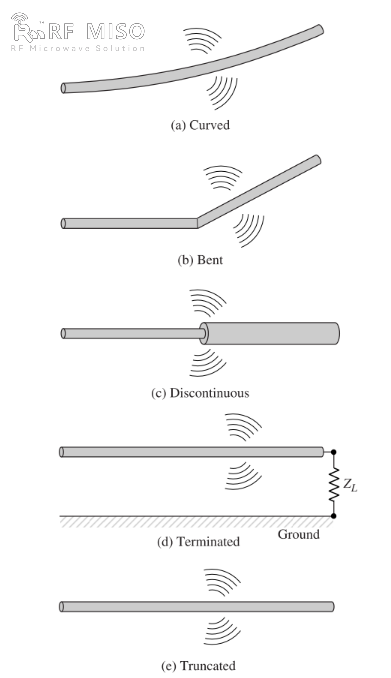
b. ଚିତ୍ର 2 ରେ ଦେଖାଯାଇଥିବା ପରି ଯଦି ତାରଟି ବଙ୍କା, ଫୋଲ୍ଡ କିମ୍ବା ବିଚ୍ଛିନ୍ନ ହୋଇଥାଏ, ତେବେ ବିକିରଣ ହୁଏ।
୩) ଯଦି ସମୟ ସହିତ ଚାର୍ଜ ଦୋଳନଶୀଳ ହୁଏ, ତେବେ ତାର ସିଧା ଥିଲେ ମଧ୍ୟ ଚାର୍ଜ ବିକିରଣ କରିବ।
ଚିତ୍ର ୨
ଚିତ୍ର 2(d) ରେ ଦେଖାଯାଇଥିବା ପରି, ଏକ ଖୋଲା ତାର ସହିତ ସଂଯୁକ୍ତ ଏକ ସ୍ପନ୍ଦିତ ଉତ୍ସକୁ ଦେଖି ବିକିରଣ ଯନ୍ତ୍ରର ଗୁଣାତ୍ମକ ବୁଝାମଣା ହାସଲ କରାଯାଇପାରିବ, ଯାହାକୁ ତାରର ଖୋଲା ମୁଣ୍ଡରେ ଏକ ଭାର ମାଧ୍ୟମରେ ଗ୍ରାଉଣ୍ଡ କରାଯାଇପାରିବ। ଯେତେବେଳେ ତାର ପ୍ରାରମ୍ଭିକ ଭାବରେ ଶକ୍ତିପ୍ରାପ୍ତ ହୁଏ, ତାରରେ ଥିବା ଚାର୍ଜ (ମୁକ୍ତ ଇଲେକ୍ଟ୍ରନ) ଉତ୍ସ ଦ୍ୱାରା ସୃଷ୍ଟି ହୋଇଥିବା ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖା ଦ୍ୱାରା ଗତିରେ ସ୍ଥିର ହୁଏ। ଯେହେତୁ ତାରର ଉତ୍ସ ମୁଣ୍ଡରେ ଚାର୍ଜଗୁଡ଼ିକ ତ୍ୱରାନ୍ୱିତ ହୁଏ ଏବଂ ତାରର ଶେଷ ମୁଣ୍ଡରେ ପ୍ରତିଫଳିତ ହେଲେ ହ୍ରାସ ପାଏ (ମୂଳ ଗତି ତୁଳନାରେ ଋଣାତ୍ମକ ତ୍ୱରାନ୍ୱିତ), ଏହାର ଶେଷ ମୁଣ୍ଡରେ ଏବଂ ତାରର ଅବଶିଷ୍ଟ ଅଂଶ ସହିତ ଏକ ବିକିରଣ କ୍ଷେତ୍ର ସୃଷ୍ଟି ହୁଏ। ଚାର୍ଜଗୁଡ଼ିକର ତ୍ୱରାନ୍ୱୟ ଏକ ବାହ୍ୟ ଶକ୍ତି ଉତ୍ସ ଦ୍ୱାରା ସମ୍ପାଦିତ ହୁଏ ଯାହା ଚାର୍ଜଗୁଡ଼ିକୁ ଗତିରେ ସ୍ଥିର କରେ ଏବଂ ସମ୍ପୃକ୍ତ ବିକିରଣ କ୍ଷେତ୍ର ଉତ୍ପାଦନ କରେ। ତାରର ଶେଷ ମୁଣ୍ଡରେ ଚାର୍ଜଗୁଡ଼ିକର ହ୍ରାସ ପ୍ରେରିତ କ୍ଷେତ୍ର ସହିତ ଜଡିତ ଆଭ୍ୟନ୍ତରୀଣ ଶକ୍ତି ଦ୍ୱାରା ସମ୍ପାଦିତ ହୁଏ, ଯାହା ତାରର ଶେଷ ମୁଣ୍ଡରେ କେନ୍ଦ୍ରିତ ଚାର୍ଜଗୁଡ଼ିକର ସଂଗ୍ରହ ଦ୍ୱାରା ହୋଇଥାଏ। ଆଭ୍ୟନ୍ତରୀଣ ବଳଗୁଡ଼ିକ ଚାର୍ଜ ସଂଗ୍ରହରୁ ଶକ୍ତି ଲାଭ କରନ୍ତି କାରଣ ତାରର ଶେଷ ମୁଣ୍ଡରେ ଏହାର ବେଗ ଶୂନ୍ୟକୁ ହ୍ରାସ ପାଏ। ତେଣୁ, ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଉତ୍ତେଜନା ଯୋଗୁଁ ଚାର୍ଜର ତ୍ୱରାନ୍ୱିତତା ଏବଂ ତାର ପ୍ରତିରୋଧର ବିଚ୍ଛିନ୍ନତା କିମ୍ବା ସୁଗମ ବକ୍ର ଯୋଗୁଁ ଚାର୍ଜର ହ୍ରାସ ହେଉଛି ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ବିକିରଣ ସୃଷ୍ଟି ପାଇଁ ଯନ୍ତ୍ର। ଯଦିଓ ମ୍ୟାକ୍ସୱେଲଙ୍କ ସମୀକରଣରେ ଉଭୟ ବିଦ୍ୟୁତ୍ ଘନତ୍ୱ (Jc) ଏବଂ ଚାର୍ଜ ଘନତ୍ୱ (qv) ଉତ୍ସ ଶବ୍ଦ, ଚାର୍ଜକୁ ଅଧିକ ମୌଳିକ ପରିମାଣ ଭାବରେ ବିବେଚନା କରାଯାଏ, ବିଶେଷକରି କ୍ଷଣସ୍ଥାୟୀ କ୍ଷେତ୍ର ପାଇଁ। ଯଦିଓ ବିକିରଣର ଏହି ବ୍ୟାଖ୍ୟା ମୁଖ୍ୟତଃ କ୍ଷଣସ୍ଥାୟୀ ଅବସ୍ଥା ପାଇଁ ବ୍ୟବହୃତ ହୁଏ, ଏହାକୁ ସ୍ଥିର-ଅବସ୍ଥା ବିକିରଣ ବ୍ୟାଖ୍ୟା କରିବାକୁ ମଧ୍ୟ ବ୍ୟବହାର କରାଯାଇପାରିବ।
ଅନେକ ଉତ୍କୃଷ୍ଟ ସୁପାରିଶ କରନ୍ତୁଆଣ୍ଟେନା ଉତ୍ପାଦଗୁଡ଼ିକଦ୍ୱାରା ନିର୍ମିତଆରଏଫଏମଆଇଏସଓ:
୨. ଦୁଇ-ତାର ବିକିରଣ
ଚିତ୍ର 3(a) ରେ ଦେଖାଯାଇଥିବା ପରି, ଏକ ଆଣ୍ଟେନା ସହିତ ସଂଯୁକ୍ତ ଏକ ଦୁଇ-ପରିବାହୀ ପରିବହନ ଲାଇନ ସହିତ ଏକ ଭୋଲଟେଜ ଉତ୍ସ ସଂଯୋଗ କରନ୍ତୁ। ଦୁଇ-ତାର ରେଖାରେ ଭୋଲଟେଜ ପ୍ରୟୋଗ କରିବା ଦ୍ୱାରା ପରିବାହୀ ମଧ୍ୟରେ ଏକ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ସୃଷ୍ଟି ହୁଏ। ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକ ପ୍ରତ୍ୟେକ ପରିବାହୀ ସହିତ ସଂଯୁକ୍ତ ମୁକ୍ତ ଇଲେକ୍ଟ୍ରନଗୁଡ଼ିକ (ପରମାଣୁରୁ ସହଜରେ ପୃଥକ) ଉପରେ କାର୍ଯ୍ୟ କରନ୍ତି ଏବଂ ସେମାନଙ୍କୁ ଗତି କରିବାକୁ ବାଧ୍ୟ କରନ୍ତି। ଚାର୍ଜର ଗତି କରେଣ୍ଟ ସୃଷ୍ଟି କରେ, ଯାହା ପରେ ଏକ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୃଷ୍ଟି କରେ।
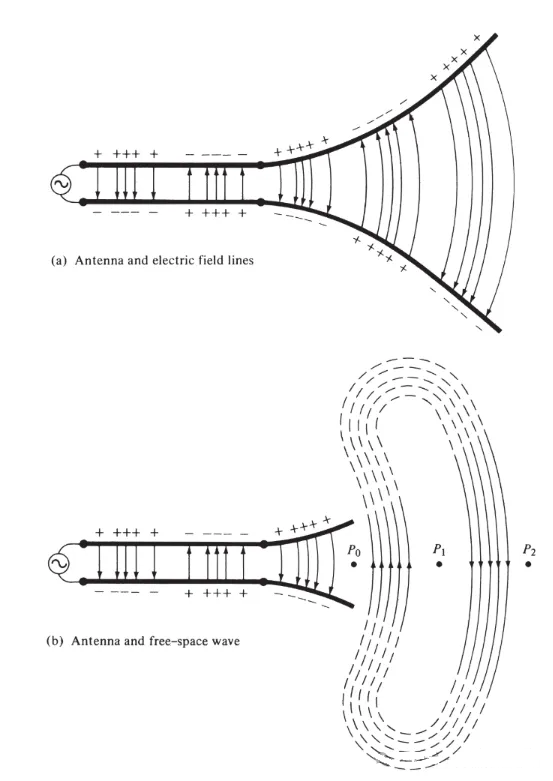
ଚିତ୍ର 3
ଆମେ ସ୍ୱୀକାର କରିଛୁ ଯେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକ ଧନାତ୍ମକ ଚାର୍ଜ ସହିତ ଆରମ୍ଭ ହୋଇ ଋଣାତ୍ମକ ଚାର୍ଜ ସହିତ ଶେଷ ହୁଏ। ନିଶ୍ଚିତ ଭାବରେ, ସେମାନେ ଧନାତ୍ମକ ଚାର୍ଜ ସହିତ ଆରମ୍ଭ ହୋଇ ଅନନ୍ତରେ ଶେଷ ହୋଇପାରନ୍ତି; କିମ୍ବା ଅନନ୍ତରେ ଆରମ୍ଭ ହୋଇ ଋଣାତ୍ମକ ଚାର୍ଜ ସହିତ ଶେଷ ହୋଇପାରନ୍ତି; କିମ୍ବା ବନ୍ଦ ଲୁପ୍ ଗଠନ କରନ୍ତି ଯାହା କୌଣସି ଚାର୍ଜ ସହିତ ଆରମ୍ଭ କିମ୍ବା ଶେଷ ହୁଏ ନାହିଁ। ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକ ସର୍ବଦା କରେଣ୍ଟ-ବାହକ କଣ୍ଡକ୍ଟର ଚାରିପାଖରେ ବନ୍ଦ ଲୁପ୍ ଗଠନ କରନ୍ତି କାରଣ ପଦାର୍ଥ ବିଜ୍ଞାନରେ କୌଣସି ଚୁମ୍ବକୀୟ ଚାର୍ଜ ନାହିଁ। କିଛି ଗାଣିତିକ ସୂତ୍ରରେ, ଶକ୍ତି ଏବଂ ଚୁମ୍ବକୀୟ ଉତ୍ସ ସହିତ ଜଡିତ ସମାଧାନ ମଧ୍ୟରେ ଦ୍ୱୈତତା ଦେଖାଇବା ପାଇଁ ସମାନ ଚୁମ୍ବକୀୟ ଚାର୍ଜ ଏବଂ ଚୁମ୍ବକୀୟ କରେଣ୍ଟ ପ୍ରଚଳନ କରାଯାଏ।
ଦୁଇଟି ପରିବାହୀ ମଧ୍ୟରେ ଅଙ୍କିତ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖା ଚାର୍ଜ ବଣ୍ଟନ ଦେଖାଇବାରେ ସାହାଯ୍ୟ କରେ। ଯଦି ଆମେ ଧରିନେବା ଯେ ଭୋଲଟେଜ ଉତ୍ସ ସାଇନସୋଏଡାଲ୍, ତେବେ ଆମେ ଆଶା କରୁ ଯେ ପରିବାହୀ ମଧ୍ୟରେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ମଧ୍ୟ ସାଇନସୋଏଡାଲ୍ ହେବ ଏବଂ ଉତ୍ସର ଅବଧି ସମାନ ହେବ। ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ଶକ୍ତିର ଆପେକ୍ଷିକ ପରିମାଣ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାର ଘନତା ଦ୍ୱାରା ପ୍ରତିନିଧିତ୍ୱ କରାଯାଏ, ଏବଂ ତୀରଗୁଡ଼ିକ ଆପେକ୍ଷିକ ଦିଗ (ଧନାତ୍ମକ କିମ୍ବା ଋଣାତ୍ମକ) ସୂଚାଇଥାଏ। ପରିବାହୀ ମଧ୍ୟରେ ସମୟ-ପରିବର୍ତ୍ତିତ ବୈଦ୍ୟୁତିକ ଏବଂ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ସୃଷ୍ଟି ଏକ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ଗଠନ କରେ ଯାହା ଟ୍ରାନ୍ସମିସନ୍ ରେଖା ସହିତ ପ୍ରସାରିତ ହୁଏ, ଯେପରି ଚିତ୍ର 3(a) ରେ ଦେଖାଯାଇଛି। ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ଚାର୍ଜ ଏବଂ ଅନୁରୂପ କରେଣ୍ଟ ସହିତ ଆଣ୍ଟେନାରେ ପ୍ରବେଶ କରେ। ଯଦି ଆମେ ଆଣ୍ଟେନା ଗଠନର କିଛି ଅଂଶକୁ କାଢ଼ି ଦେଉ, ଯେପରି ଚିତ୍ର 3(b) ରେ ଦେଖାଯାଇଛି, ତେବେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାର ଖୋଲା ପ୍ରାନ୍ତଗୁଡ଼ିକୁ "ସଂଯୋଗ" କରି ଏକ ମୁକ୍ତ-ସ୍ଥାନ ତରଙ୍ଗ ସୃଷ୍ଟି ହୋଇପାରିବ (ବିନ୍ଦୁଯୁକ୍ତ ରେଖା ଦ୍ୱାରା ଦେଖାଯାଇଛି)। ମୁକ୍ତ-ସ୍ଥାନ ତରଙ୍ଗ ମଧ୍ୟ ପର୍ଯ୍ୟାୟଗତ, କିନ୍ତୁ ସ୍ଥିର-ଅବଧି ବିନ୍ଦୁ P0 ଆଲୋକର ବେଗରେ ବାହାରକୁ ଗତି କରେ ଏବଂ ଅଧା ସମୟ ମଧ୍ୟରେ λ/2 (P1 ପର୍ଯ୍ୟନ୍ତ) ଦୂରତା ଯାତ୍ରା କରେ। ଆଣ୍ଟେନା ନିକଟରେ, ସ୍ଥିର-ଫେଜ୍ ବିନ୍ଦୁ P0 ଆଲୋକର ବେଗ ଅପେକ୍ଷା ଦ୍ରୁତ ଗତିରେ ଗତି କରେ ଏବଂ ଆଣ୍ଟେନାଠାରୁ ଦୂରରେ ଥିବା ବିନ୍ଦୁଗୁଡ଼ିକରେ ଆଲୋକର ବେଗ ନିକଟକୁ ଯାଏ। ଚିତ୍ର 4 ଟି t = 0, t/8, t/4, ଏବଂ 3T/8 ରେ λ∕2 ଆଣ୍ଟେନାର ମୁକ୍ତ-ସ୍ଥାନ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ବଣ୍ଟନ ଦର୍ଶାଉଛି।
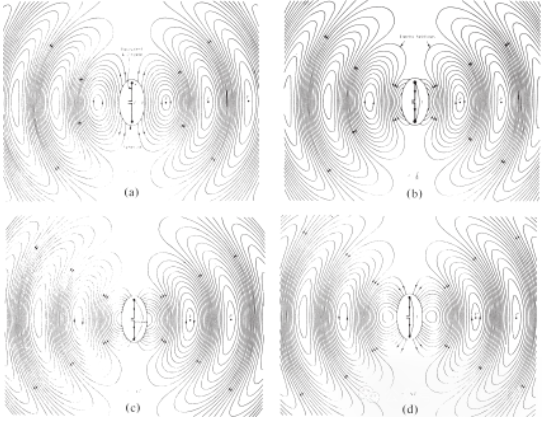
ଚିତ୍ର 4 t = 0, t/8, t/4 ଏବଂ 3T/8 ରେ λ∕2 ଆଣ୍ଟେନାର ମୁକ୍ତ ସ୍ଥାନ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ବଣ୍ଟନ
ଏହା ଜଣାନାହିଁ ଯେ ନିର୍ଦ୍ଦେଶିତ ତରଙ୍ଗଗୁଡ଼ିକ ଆଣ୍ଟେନାରୁ କିପରି ପୃଥକ ହୁଏ ଏବଂ ଶେଷରେ ମୁକ୍ତ ସ୍ଥାନରେ ପ୍ରସାରିତ ହେବା ପାଇଁ ଗଠିତ ହୁଏ। ଆମେ ନିର୍ଦ୍ଦେଶିତ ଏବଂ ମୁକ୍ତ ସ୍ଥାନ ତରଙ୍ଗଗୁଡ଼ିକୁ ଜଳ ତରଙ୍ଗ ସହିତ ତୁଳନା କରିପାରିବା, ଯାହା ଶାନ୍ତ ଜଳଭାଗରେ ପଡ଼ିଥିବା ପଥର କିମ୍ବା ଅନ୍ୟ ଉପାୟରେ ହୋଇପାରେ। ପାଣିରେ ବିଭ୍ରାଟ ଆରମ୍ଭ ହେବା ପରେ, ଜଳ ତରଙ୍ଗ ସୃଷ୍ଟି ହୁଏ ଏବଂ ବାହାରକୁ ପ୍ରସାରିତ ହେବା ଆରମ୍ଭ କରେ। ବିଭ୍ରାଟ ବନ୍ଦ ହେଲେ ମଧ୍ୟ, ତରଙ୍ଗଗୁଡ଼ିକ ବନ୍ଦ ହୁଏ ନାହିଁ ବରଂ ଆଗକୁ ପ୍ରସାରିତ ହେବା ଜାରି ରଖେ। ଯଦି ବିଭ୍ରାଟ ଜାରି ରହେ, ତେବେ ନୂତନ ତରଙ୍ଗଗୁଡ଼ିକ ନିରନ୍ତର ସୃଷ୍ଟି ହୁଏ, ଏବଂ ଏହି ତରଙ୍ଗଗୁଡ଼ିକର ପ୍ରସାରଣ ଅନ୍ୟ ତରଙ୍ଗ ଅପେକ୍ଷା ପଛରେ ପଡ଼ିଯାଏ।
ବୈଦ୍ୟୁତିକ ବିଭ୍ରାଟ ଦ୍ୱାରା ସୃଷ୍ଟି ହୋଇଥିବା ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ପାଇଁ ମଧ୍ୟ ସମାନ କଥା। ଯଦି ଉତ୍ସରୁ ପ୍ରାରମ୍ଭିକ ବୈଦ୍ୟୁତିକ ବିଭ୍ରାଟ ସ୍ୱଳ୍ପକାଳୀନ ହୋଇଥାଏ, ତେବେ ସୃଷ୍ଟି ହୋଇଥିବା ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ପରିବହନ ରେଖା ଭିତରେ ପ୍ରସାରିତ ହୁଏ, ତା'ପରେ ଆଣ୍ଟେନାରେ ପ୍ରବେଶ କରେ ଏବଂ ଶେଷରେ ମୁକ୍ତ ସ୍ଥାନ ତରଙ୍ଗ ଭାବରେ ବିକିରଣ କରେ, ଯଦିଓ ଉତ୍ତେଜନା ଆଉ ଉପସ୍ଥିତ ନଥାଏ (ଜଳ ତରଙ୍ଗ ଏବଂ ସେମାନେ ସୃଷ୍ଟି କରିଥିବା ବିଭ୍ରାଟ ପରି)। ଯଦି ବୈଦ୍ୟୁତିକ ବିଭ୍ରାଟ ନିରନ୍ତର ଥାଏ, ତେବେ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ନିରନ୍ତର ଭାବରେ ଅବସ୍ଥିତ ଏବଂ ପ୍ରସାର ସମୟରେ ସେମାନଙ୍କ ପଛକୁ ଘୁଞ୍ଚିଥାଏ, ଯେପରି ଚିତ୍ର 5 ରେ ଦେଖାଯାଇଥିବା ବାଇକୋନିକାଲ୍ ଆଣ୍ଟେନାରେ ଦର୍ଶାଯାଇଛି। ଯେତେବେଳେ ବିଦ୍ୟୁତ୍-ଚୁମ୍ବକୀୟ ତରଙ୍ଗ ପରିବହନ ରେଖା ଏବଂ ଆଣ୍ଟେନା ଭିତରେ ଥାଏ, ସେମାନଙ୍କର ଅସ୍ତିତ୍ୱ ପରିବାହୀ ଭିତରେ ବୈଦ୍ୟୁତିକ ଚାର୍ଜର ଅସ୍ତିତ୍ୱ ସହିତ ଜଡିତ। ତଥାପି, ଯେତେବେଳେ ତରଙ୍ଗ ବିକିରଣ ହୁଏ, ସେମାନେ ଏକ ବନ୍ଦ ଲୁପ୍ ଗଠନ କରନ୍ତି ଏବଂ ସେମାନଙ୍କର ଅସ୍ତିତ୍ୱ ବଜାୟ ରଖିବା ପାଇଁ କୌଣସି ଚାର୍ଜ ନଥାଏ। ଏହା ଆମକୁ ଏହି ନିଷ୍କର୍ଷକୁ ନେଇଯାଏ ଯେ:
କ୍ଷେତ୍ରର ଉତ୍ତେଜନା ପାଇଁ ଚାର୍ଜର ତ୍ୱରାନ୍ୱିତ ଏବଂ ହ୍ରାସ ଆବଶ୍ୟକ, କିନ୍ତୁ କ୍ଷେତ୍ରର ରକ୍ଷଣାବେକ୍ଷଣ ପାଇଁ ଚାର୍ଜର ତ୍ୱରାନ୍ୱିତ ଏବଂ ହ୍ରାସ ଆବଶ୍ୟକ ନୁହେଁ।
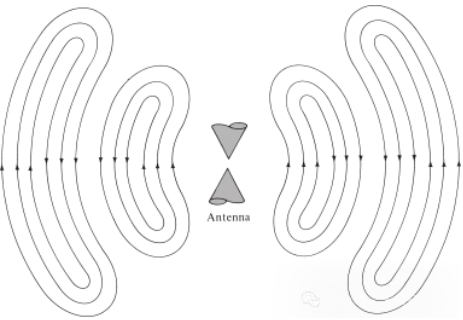
ଚିତ୍ର 5
୩. ଡାଇପୋଲ୍ ବିକିରଣ
ଆମେ ସେହି ଯନ୍ତ୍ରକୁ ବ୍ୟାଖ୍ୟା କରିବାକୁ ଚେଷ୍ଟା କରୁ ଯାହା ଦ୍ୱାରା ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକ ଆଣ୍ଟେନାରୁ ଅଲଗା ହୋଇ ମୁକ୍ତ-ସ୍ଥାନ ତରଙ୍ଗ ସୃଷ୍ଟି କରନ୍ତି, ଏବଂ ଏକ ଉଦାହରଣ ଭାବରେ ଦ୍ୱିପୋଲ ଆଣ୍ଟେନାକୁ ନେଇଥାଉ। ଯଦିଓ ଏହା ଏକ ସରଳୀକୃତ ବ୍ୟାଖ୍ୟା, ଏହା ଲୋକଙ୍କୁ ଅନ୍ତର୍ନିହିତ ଭାବରେ ମୁକ୍ତ-ସ୍ଥାନ ତରଙ୍ଗର ସୃଷ୍ଟିକୁ ଦେଖିବାରେ ମଧ୍ୟ ସକ୍ଷମ କରିଥାଏ। ଚିତ୍ର 6(a) ଚକ୍ରର ପ୍ରଥମ ତ୍ରୟମାସରେ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକ λ∕4 ଦ୍ୱାରା ବାହାରକୁ ଗତି କରିବା ସମୟରେ ଦ୍ୱିପୋଲର ଦୁଇ ବାହୁ ମଧ୍ୟରେ ସୃଷ୍ଟି ହୋଇଥିବା ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକୁ ଦର୍ଶାଉଛି। ଏହି ଉଦାହରଣ ପାଇଁ, ଆସନ୍ତୁ ଧରିନେବା ଯେ ଗଠିତ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖା ସଂଖ୍ୟା 3। ଚକ୍ରର ପରବର୍ତ୍ତୀ ତ୍ରୟମାସରେ, ମୂଳ ତିନୋଟି ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖା ଅନ୍ୟ λ∕4 (ଆରମ୍ଭ ବିନ୍ଦୁରୁ ମୋଟ λ∕2) ଘୁଞ୍ଚାଏ, ଏବଂ ପରିବାହକ ଉପରେ ଚାର୍ଜ ଘନତା ହ୍ରାସ ପାଇବାକୁ ଆରମ୍ଭ କରେ। ଏହାକୁ ବିପରୀତ ଚାର୍ଜ ପ୍ରବର୍ତ୍ତନ ଦ୍ୱାରା ଗଠିତ ବୋଲି ବିବେଚନା କରାଯାଇପାରିବ, ଯାହା ଚକ୍ରର ପ୍ରଥମାର୍ଦ୍ଧ ଶେଷରେ ପରିବାହକ ଉପରେ ଚାର୍ଜକୁ ବାତିଲ କରିଥାଏ। ବିପରୀତ ଚାର୍ଜ ଦ୍ୱାରା ସୃଷ୍ଟି ହୋଇଥିବା ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକ 3 ଏବଂ λ∕4 ଦୂରତା ଘୁଞ୍ଚାଏ, ଯାହାକୁ ଚିତ୍ର 6(b) ରେ ବିନ୍ଦୁଯୁକ୍ତ ରେଖା ଦ୍ୱାରା ଦର୍ଶାଯାଇଛି।
ଶେଷ ଫଳାଫଳ ହେଉଛି ଯେ ପ୍ରଥମ λ∕4 ଦୂରତାରେ ତିନୋଟି ନିମ୍ନଗାମୀ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖା ଏବଂ ଦ୍ୱିତୀୟ λ∕4 ଦୂରତାରେ ସମାନ ସଂଖ୍ୟକ ଉପରଗାମୀ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖା ଅଛି। ଯେହେତୁ ଆଣ୍ଟେନାରେ କୌଣସି ନେଟ୍ ଚାର୍ଜ ନାହିଁ, ତେଣୁ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକୁ ପରିବାହୀଠାରୁ ପୃଥକ କରିବାକୁ ଏବଂ ଏକ ବନ୍ଦ ଲୁପ୍ ଗଠନ କରିବାକୁ ବାଧ୍ୟ କରିବାକୁ ପଡିବ। ଏହା ଚିତ୍ର 6(c) ରେ ଦେଖାଯାଇଛି। ଦ୍ୱିତୀୟାର୍ଦ୍ଧରେ, ସମାନ ଭୌତିକ ପ୍ରକ୍ରିୟା ଅନୁସରଣ କରାଯାଏ, କିନ୍ତୁ ଧ୍ୟାନ ଦିଅନ୍ତୁ ଯେ ଦିଗଟି ବିପରୀତ। ଏହା ପରେ, ପ୍ରକ୍ରିୟାଟି ପୁନରାବୃତ୍ତି ହୁଏ ଏବଂ ଅନିର୍ଦ୍ଦିଷ୍ଟ କାଳ ପାଇଁ ଜାରି ରହେ, ଚିତ୍ର 4 ପରି ଏକ ବୈଦ୍ୟୁତିକ କ୍ଷେତ୍ର ବଣ୍ଟନ ଗଠନ କରେ।
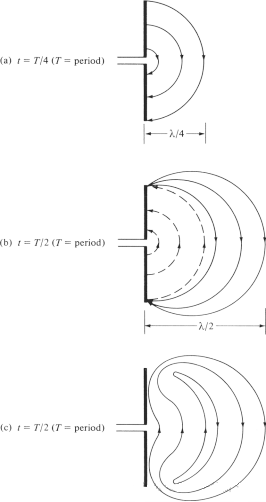
ଚିତ୍ର 6
ଆଣ୍ଟେନା ବିଷୟରେ ଅଧିକ ଜାଣିବା ପାଇଁ, ଦୟାକରି ପରିଦର୍ଶନ କରନ୍ତୁ:
ପୋଷ୍ଟ ସମୟ: ଜୁନ୍-୨୦-୨୦୨୪










